一道物理题中的平移不变性
最近看到一道很有意思的物理竞赛题,题面是这样的:
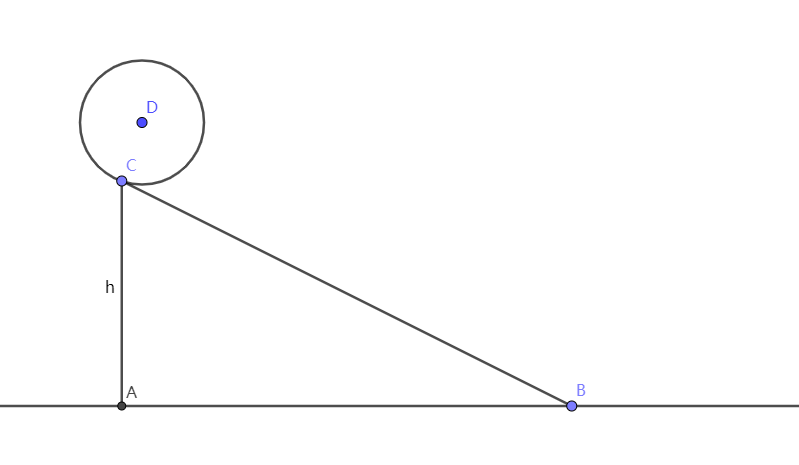
一高为 \(h\) 的斜面固定在地面上,从顶部释放一小球。一观察者乘坐火车以速度 \(v_0\) 匀速经过,请问小球的机械能对于该观察者是否守恒?
先公布答案:不守恒。
是不是感觉很意外?
现在给出该题的标准题解:若我们静止在地面上观察,那么小球的重力势能显然都将转化为动能,具体来说应该是这样:
\[ mgh=\dfrac{1}{2}mv^{2} \]
此时小球机械能守恒。
若参考系以速度 \(v_0\) 匀速运动,那么小球初始状态下动能为
\[ E_{k_{0}}=\dfrac{1}{2}mv_{0}^{2} \]
在斜面底端时动能为
\[ \begin{aligned}E_{k1}&=\dfrac{1}{2}m\left( v+v_{0}\right) ^{2}\\ &=\dfrac{1}{2}mv^{2}+mv\cdot v_{0}+\dfrac{1}{2}mv_{0}^{2}\\ &=mgh+\dfrac{1}{2}mv_{0}^{2}+mv\cdot v_{0}\\ \end{aligned} \]
可以看到,在底端时动能表达式中除了重力势能和初始动能,还多了一项:\(mv\cdot v_{0}\). 因此机械能不守恒,证毕。
然而,我相信大多数人都像我一样,看到题解后仍然无法接受小球机械能不守恒的情况。为什么一个这么重要的守恒定律,仅仅变换了一个参考系就被破坏了?更严重的是,为什么一个匀速运动的参考系会出现和静止参考系不一样的现象?难道说,绝对静止是存在的?
所以我们将仔细审视我们自己「想当然」的思路,逐步排查出这里究竟是哪一部分出了问题。
首先,我们回头看看题解中的最后一条式子。看起来,这里出问题的根源在于那个平方项。正是由于这里是 \(v^2\) ,所以速度的线性叠加并不等于动能的线性叠加,也就在后面冒出了一个 \(mv\cdot v_{0}\) 。所以,我们从功的角度来看这个问题。显然,小球在两个参考系中受力情况是相同的。然而要注意到,小球所受的支持力在静止参考系下是与运动方向垂直的,因而不做功;但在匀速运动的参考系下,小球速度叠加了参考系的速度 \(v_0\) ,因而支持力将对小球做功。看起来,问题就出在这上面了。我们可以尝试着计算支持力做的功:
\[ \begin{aligned}W&=F_{T}\cdot s\\ &=F_{T}\cdot v_{0}t\\ &=G\cos \theta t\cdot v_{0}\\ &=mv\cdot v_{0}\end{aligned} \]
(注解:由受力分析可以看出,支持力与重力沿斜面向下的分力,对水平方向也即 \(v_0\) 方向的投影是相同的)
结果和预想的一样。另外,注意到我们这里使用了动能定理。
但我们知道,力是相互作用的。那么一个功也应该有一个与之对应的相反的功。在这里,相反的功是什么呢?是小球对斜面做的负功(在这里假设 \(v_0\) 与小球运动方向同向了,若反向,正负功也将颠倒)。原来,在这个过程中小球的一部分动能来源于斜面!当我们把斜面和小球纳入一个系统当中时,立刻就会发现两个功抵消了,此系统是机械能守恒的。
然而为什么静止时单独小球就已经是机械能守恒的呢?这是因为斜面是固定在地面上的,而我们所谓的「静止」指的正是以地面为参考系。但实际上,斜面,包括与之连通的地面,在这个过程中动能发生了变化,即使那个变化如此不起眼以至于我们常常忽略它,在这里它确实造成了「小球自己的机械能守恒」的假象。
至此,答案已经很明显了:我们以为的那个「静止」的参考系并不是惯性系,而是随着斜面一起运动。当我们去掉斜面固定在桌面上这一条件时,情况就很明显了。小球自己的机械能并不守恒,它的一部分重力势能到了斜面的动能中。而站在斜面上看到的小球机械能守恒,不过是绑定于这种参考系的一个特殊情况。
不过这里我们还能得到一个猜想。注意到我们刚才推导支持力做功时使用了动能定理,而在将斜面纳入系统中时正好把它抵消了。这正好对应着斜面和小球组成的系统是遵守动量守恒的。那么,是不是所有动量守恒的系统,在匀速运动的参考系下能量都是不变的呢?事实上确实是这样!功是力在位移上的累积,而匀速参考系之速度改变对应着位移的改变。当一个力的反作用力也被考虑到系统中,两边位移的改变才能正好抵消。这,就是「空间平移不变性」了。
References
Related Links